[Home Page]
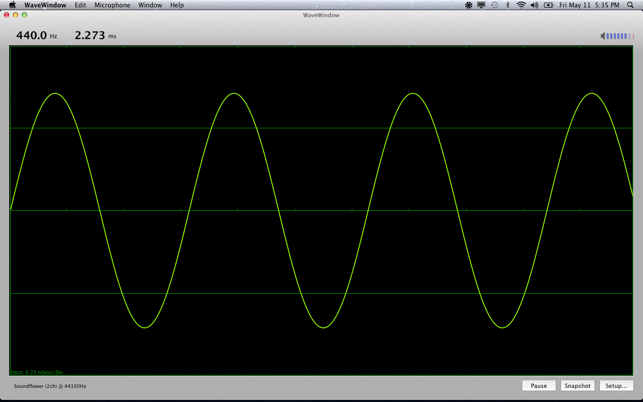
WaveWindow AU is an Audio Units plug-in software oscilloscope. Category: Developer: Laidman & Katsura - Download - Price: - rustykat - homepage - rustle laidman - hidemoto katsura - guitar; Vocal Lab AU v.1.1.2. Vocal Lab AU is an Audio Units plug-in version of. Laidman & Katsura release Vocal Lab AU and WaveWindow AU v2.0 (inc. Laidman & Katsura update tuner Audio Units to v1.1.2. August 18, 2006. Audio Units plug-in software oscilloscope. Audio app based on paradigms of granular synthesis. Simple sound file player. Thank you for downloading WaveWindow AU for Mac from our software portal. The version of the Mac application you are about to download is 2.2. The license type of the downloaded software for Mac OS X is shareware. This license type may impose certain restrictions on functionality or only provide an evaluation period. WaveWindow is a shareware A screen from WaveWindow 'oscilloscope' similar to the above but a little less flexible.
Physics in Context
Electronics:
Transducers, Analogue, Digital, Computers . . . the lot!
Jon M Pearce
School of Physics
The University of Melbourne
Wednesday November 2nd, 1994
Introduction
This talk concerns electronics (!). I will make no attempt to cover, nor even carefully define, the current VCE study guide. In fact I shall weave in and out of the relevant topics. My aim is to present some electronics that you may or may not be familiar with and to link it to some practical circuits. Even just skirting around the expectations of VCE Physics presents numerous possibilities. Hence, I plan to focus on a theme and try to apply it to the areas of both analogue and digital electronics.
The theme is transducers. Without them, there is no point in electronics--we have no way of sensing what it does, and no way of telling it what to do!
Part A. Analogue Circuits
Much of the VCE Physics topic Electronics Systems deals with some fairly basic electric circuit theory which most of you, as teachers, will be very familiar with: AC voltages and currents, diodes, voltage dividers, capacitive circuits, etc. Transducers are mentioned, as are amplifiers--although amplifiers are not expected to be addressed in any detail. So let's spend some time looking more deeply at amplifiers and work up to some practical circuits which might be useful for a variety of tasks, but in particular for amplifying the output of a transducer.
But wait! First a quick refresher of some basics. And then, we had better take a look at a couple of transducers.
A1 Starting with basics
We will begin by examining the simple voltage divider and consider how it shares a voltage presented by a battery across two components (resistors, in this case). The 'warm up' exercise in the talk is really to remind you that even this simple idea will cause confusion with some students and needs to be carefully worked on. It also serves to introduce the simple circuit that can be used to obtain a changing voltage from a transducer's changing parameter.
Remember that the voltage at the output of this circuit is given by the potential divider expression:
Vout = f(Rtrans R1 ,Rtrans + R1) Vin
where Rtrans is the resistance of the transducer. As the resistance of the transducer changes, due to changes in the physical property which it responds to, so too does the transducer's 'share' of the applied voltage. Note, however, that Vout does not vary linearly with changes in Rtrans. Linearity is approximate and quite good for relatively small changes in Rtrans compared to R1. The graph below shows Vout plotted as a function of Rtrans for R1 = 100[[Omega]] and Vin = 1 Volt. Note how the graph only appoximates a straight line at the point where Rtrans = Rin = 100[[Omega]]. This appoximation is, of course, better if we make Rtrans larger compared to R1. The consequence of that is, however, that the slope of the curve is smaller, ie. we get a smaller output voltage change for a given change in Rtrans: a reduced sensitivity.
Nevertheless, this is a simple and useful circuit for playing around with transducers
A2 Sensing the world
(a) Transducers
Some simple, easy to use, transducers that can be used in a voltage divider circuit like the above are:
thermistor: a semiconductor device usually with a negative temperature coefficient, meaning that its resistance will decrease as temperature increases. A typical thermistor might have a resistance of 5 k[[Omega]] at 0 oC and 100 [[Omega]] at 100o C.
light dependent resistor: just what it says--its resistance changes depending on the illumination. Common LDRs are made from CdS whose resistance decreases as light intensity increases.
phototransistor: a semiconductor device whose conduction increases with illumination. Devices vary, but a good starting point in using a phototransistor is to use a 5 k[[Omega]] resistor as R1 in the voltage divider circuit.
piezoelectric film: this amazing film produces a voltage when stressed (also when heated, illuminated, spoken to, you name it!). It can be used to monitor impacts, vibrations, infrared radiation . . . we will look at some during the lecture. Notes on this material are attached. This is not a simple resistive device, it actually generates a voltage. Hence it need not be used with a voltage divider circuit, but, since it only produces a very small amount of charge (effectively, it's a capacitor), it requires some buffering at its output. An amplifier maybe . . .
temperature sensor LM35: this wonderful IC is a three-terminal device which outputs a voltage directly proportional to the temperature in degrees centigrade. Being three-terminal, it requires no extra resistor--just apply a voltage (4 to 30 volts) and monitor the output. The sensitivity is 10 mV/oC. That's not very much! We are going to need that amplifier . . .
(b) Amplifiers
This next part of these notes presents a little theory about operational amplifiers and designing circuits using them. Then we will return to our sensor circuits and see how these amplifiers can be used.
The Ideal Operational Amplifier (Op Amp)
The op amp is an extremely useful, versatile and cheap (about $1 upwards) building block in electronics. It now is far more useful than the humble transistor (of which it comprises 20 or 30). It is used as the heart of many circuits and, as you might expect, there are now many different types for different purposes (hundreds ranging from the very cheap to very expensive). The one we will look at here is the most common one, designated 741.
The op amp is an integrated circuit with two inputs and one output. The general idea is that the output voltage is equal to the difference between the two input voltages amplified (made larger) somewhat (this is hence called a differential input). This amplification of the device is referred to as the gain (Ao).
In the above circuit, the two amplifier inputs are designated v+ and v- respectively, and the power supply voltages are designated +Vcc and -Vcc, respectively.
Rather than manufacture many different op amps of different value gains (as is done with resistors of different values), they are produced with as large a gain as possible (~ 105 or greater) and a clever technique known as feedback is employed to produce the exact gain you may require for a particular application.
We will not concern ourselves with the inner workings of this complex integrated circuit known as the op amp. Instead we will regard it as a black box about which we know little except for its behaviour.
Below are three important characteristics comparing an ideal op amp with the 741 that we will be using:
Note the following:

* In practice the op amp has more than three legs on the IC package. There is also a +ve and -ve power supply input, (usually +/-15 volts) as well as a couple of others besides the input & output connections.
* It is always assumed that all voltages are measured with respect to earth (zero volts).
* The maximum output voltage you can ever hope to get from an op amp is equal to the supply voltage (often a volt or so less) which is usually +15 volts.
Each of the circuits analysed below make use of feedback to convert a basic amplifier into a useful circuit. Each analysis is very similar once a few basic rules are established. The first example establishes these rules in detail, the rest assume their use.
The Inverting Amplifier
Consider the circuit below:
As will always be the case, we have assumed that the power supply is connected and have not bothered to show it in the diagram (+ 15volts). We will also assume that all voltages are measured relative to earth.
Our aim is to derive the gain for the complete circuit (i.e the closed loop gain, A).
Let us start by assuming that whatever the input, we have a sensible output, say 10 volts (remember the output must be in the range + 15 volts, the supply voltage). If this is so, then what voltage must exist between the input terminals of the op amp? Well, remember
vout = Ao(v+ - v-)
hence, v+ - v- = f(vout,Ao)
Now, no matter what the input voltage is, we know that Ao is very large (at least 105 ). Hence, from the above expression, (v+ - v-) must be very small--in fact so small that we can approximate it to being equal to zero volts for most practical purposes.
This is an extremely important concept. Let's state it again:
If the output of the circuit is to have any sensible finite value,
and Ao ~ infinity,
then v+ ~ v-
This is referred to as a virtual equality, and in this case, since v+ is connected to earth, v- must also equal earth (zero volts). Hence we call this a virtual earth.
So far we have made two assumptions regarding the op amp:
1. Ao is very large (~ infinity).
2. There is a virtual equality between the two inputs to the op amp.)
We need one more approximation regarding the input resistance to the op amp. Consider what happens to the current flowing into the op amp circuit:
Since the input resistance of the op amp is so large, we can assume that practically no current flows into v-.(i.e. no current flows into the chip itself). Hence, the input current iin must flow through RF and back to earth via the op amp or via whatever might be connected between vout and earth (or both). This makes analysis almost trivial:
iin = f(vi - v-,R)
but since v- ~ 0,
iin ~ f(vi,R) (1)
and also, from Ohm's Law, the current through RF must equal the voltage across it divided by RF, so iin is also given by
iin = f(v- - vo,RF)
=> vo = - iinRF (remember v- ~ 0)
Substituting (1) into this,
vo = f(-RF vin,R)
or f(vo,vin) = f(-RF,R) this is the closed loop gain, A
These equations tell us that the output voltage of the circuit is equal to the input voltage multiplied by the ratio -(RF/R). You can now design an amplifier circuit of any gain simply by choosing the values of two resistors! It is as simple as that. Choose RF = 10 k[[Omega]] and R = 1 k[[Omega]] and you have an amplifier of gain -10.
Note two points:
1. The gain is determined solely by the values of the resistors, not by the value of the op amp's open loop gain (Ao).
2. The gain is negative. That means in the above example, if you put +0.4 volts in, you will get -4.0 volts out. More commonly, if you put a sinusoidal signal in, you will get an inverted sinusoidal signal out.
Wave Window Valance
The Non-inverting Amplifier
An amplifier which does not invert the input signal can be analysed in similar fashion. This time we will assume the current through R to flow in the opposite direction for convenience (it does not matter as the actual direction of this current depends on whether the input signal is positive or negative).
i = f(v- ,R) ~ f(vin ,R) (virtual equality, but not virtual earth this time)
and vout = v- + iRF
= vin + f(vin RF,R)
=> vout = f(RF + R,R) vin
or f(vout, vin) = 1 + f(RF,R)
Hence for a gain of +10, you might choose RF = 9k[[Omega]] and R = 1k[[Omega]] (or 90k[[Omega]] and 10k[[Omega]], etc).
The Differential Amplifier
Prove for yourself that for the following circuit
vout = f(RF (vi2-vi1),R)
Note that here we have a virtual equality but not a virtual earth.
This is a particularly useful circuit when you have two wires, one carrying a signal you wish to amplify and one (say) earth, and they are both picking noise from a common source (maybe 50 Hz noise from the mains). The differential amplifier will amplify the signal (which is the difference between the wires) and not the noise (which is common between the wires). This circuit is commonly used in amplifiers for instrumentation use.
The Integrator
A final circuit to consider is the following:
iin = f(vin,R) (virtual earth)
and vout = - f(Q,C) (assuming Q is charge on C at any instant)
= - f(1,C) i(,iindt)
=> vout = - f(1,RC) i(,vindt)
That is, whatever the input signal looks like, the output is the (negative) integral of it!
For example, if the input is

(depending on starting conditions)
If the input is a sine wave, the output will bea cosine, i.e. shifted in phase by 90o.
Applications of this circuit include analogue computing, waveform generation, summing quantities such as time, power use, etc.
(c) Two circuits to experiment with
Let's apply some of these amplifier ideas to help with our transducer circuits.
Improving input resistance
Our basic voltage divider expression, Vout = f(Rtrans R1 ,Rtrans + R1) Vin, assumes that all the current flows through Rtrans and R1 and that none sneaks off anywhere else. This is not true if something is attached to the output of the circuit:
Even a voltmeter draws some current; the question is 'how much?'. For example, in the above circuit, if the transducer's resistance is 5k and the meter's resistance is also 5 k (typical for a large display meter) then the output voltage reduces from one half the supply voltage to one third of it.
One solution is to feed the output through a very high input resistance 'buffer' circuit. A non-inverting amplifier with gain +1 is ideal. A simple way to design such a circuit is to use resistances of value RF = 0 and R = [[infinity]]. (Where do you get such strange resistors!!)
The circuit below achieves this and has the advantage that the input resistance seen looking into the amplifier (from the transducer circuit's point of view) is simply that of the op am itself: about 1 M[[Omega]] in the case of the 741; about 1 T[[Omega]]--yes, 1012 [[Omega]]--in the case of the CA3160 op amp. This circuit is called a unity gain buffer or a voltage follower.
Amplifying a signal with a DC offset
Often the voltage divider circuit presents us with a steady DC output (of no interest) with a small changing voltage that sits on top of it. If we want to amplify that small change, we have the problem of not wanting to amplify the DC part as well (otherwise the whole signal will try to become too large and just saturate near to the supply voltage).
Here is where we can use our differential amplifier! Since this amplifier only amplifies the difference between two signals. If we make one of the inputs equal to the DC offset of the voltage divider, it will enable us to amplifier just the part of the signal that is of interest.
A good example of this arises if you want to follow temperature changes carefully over a small range. The LM35 temperature transducer produces 10mV output per degree centigrade. You might want to effectively subtract off the ambient temperature and just amplify the change from ambient. If room temperature is about 20o, then you could subtract the offending 200 millivolts by inputting 0.2 volts into the inverting input of a differential amplifier and inputting the transducer's output into the non-inverting input.
The above amplifier has a gain of one. To provide amplification we can follow it with a non-inverting amplifier of variable gain. You can't have variable gain acting on both inputs of the differential amplifier--hence the need for the second amplifier.
These three circuits, buffer, differential and variable gain, presented above can be chained together, if need be.
(d) A few practical considerations
The circuitboard used in the lecture comprises the above three amplifier circuits. However, you need to know a little more practical information in order to make such ideas work.
Power supplies
It is usual to power op amp circuit from dual supplies (a maximum of, say, +/- 15 volts, or +/-8.5 volts in the case of tha CA3160 introduced below). However, if working from batteries, it is more convenient to use a single supply (one battery, say 9 volts). This, of course, assumes that your expected output is of single polarity--not sinusoidal, for example.
The 741 op amps are not designed to do this. The CA3160, however, is a CMOS amplifier which is happy to run from a single supply. Also, being CMOS, it has an extremely high input resistance (that's good) but is susceptible to damage from static charge if not handled carefully (that's bad). We have chosen to use these CMOS amps for this circuitboard. It can be converted to run from single, rather than dual, supplies by adding a wire link to the board connecting the earth and negative supply rails together.
The board can even be used with cheaper 741 op amps, but the offset adjustment cannot then be used (see below).
Offset voltage
All op amps have a small mismatch at their inputs that cause a small voltage to appear at their outputs even if the inputs on the two inputs are zero. We are only talking about a few millivolts here, so it is often not significant.
However, if the gain of the amplifier is large (say 1000) then this offset becomes amplified and becomes a few volts! Similarly, if the gain of the amplifier is not large, but its output is going into a large gain circuit, then the same problem occurs.
The solution is either to buy a better quality op amp with specially designed low input offset voltage, or to add a potentiometer to the circuit (between pins 1 and 5) to trim the offset. The wiper of this potentiometer should attach to the positive power supply for the 741 and the negative supply rail for the CA3160. This difference means if building this particular circuit board you should not add the offset trimming potentiometers if using 741 op amps rather than CA3160.
Enough of amlpifiers. I encourage you to go away, grab a breadboard, or the circuitboard offered here, and play with them.
And now for something completely different . . .
Part B. Digitally Speaking
B1 Digital transducers
Digital transducers, by their very nature, are usually much simpler devices than analogue ones. Due to their binary nature, a digital input transducer tends to be a switch of some sort: mechanical, magnetic, optical, piezo, etc. Digital output transducers are often lights--LEDs more often than not.
This talk will not focus on these transducers other than to mention the novel range that a particular digital simulation program provides. The software, SimLog, allows you you select from push buttons, toggle switches, key pads, random number generators, LEDS, traffic lights and bells. The ultimate in output transducers is the small explosion that occurs should you connect the outputs of two gates in a fashion that leads to the destruction of the gate!
Push-button switches at input; LED at output Two gates destroyed by a wrong connection!
B2 Basic logic gates
(a) Quick review
Just to refresh your memory, we can describe the function of a basic logic gate in 5 different ways. For example, the AND gate can be described:
The basic gates are: AND, OR, NAND, NOR and NOT. Either of the two negated gates--NAND and NOR--can be used to construct any logic function.
(b) Combinational logic
Circuits can be constructed such that the combination of inputs determines the state one, or more, outputs. Being digital, this state is either ON or OFF (TRUE or FALSE, HIGH or LOW, YES or NO, 1 or 0, etc.).
Electronic lock
For example, if a unique code is required to open an electronic lock, it will be a combinational circuit that decides whether the code is correct. Let's take the example of a four bit code: using '1' to represent a HIGH logic level (+5 volts in reality) and '0' to represent a LOW logic level (0 volts), we will examine the circuit required to operate a lock only when the combination 1011 is entered.
A logical (!) approach to this is to write down the Boolean expression for the required combination. We will designate each of the 4 input bits by the letters A, B, C and D. If a logic '1' opens the lock, then we want a '1' to be the output of the circuit (f) under the following conditions:
f should equal 1 if: A is 1 AND B is 0 AND C is 1 AND D is 1
If we are going to use an AND gate for our circuit, then we should recognise that the only way to get a '1' output from an AND is if all the inputs are '1'. So, if we make the inputs to a 4-input AND gate A, xto(B), C and D, we should get a '1' out for the correct combination (the bar on top of the B means that B has been inverted, ie. the 0 that was going to the ADN gate becomes a 1).
So, our Boolean function is
f = A . xto(B) . C . D (the '.' represents the AND function; a '+' is used for OR)
and the circuit is (using a bell to represent the lock!)
If you don't have 4-input gates, then you can easily make up the equivalent using three 2-input gates:
This latter circuit is essentially regrouping the expression as:
f = (((A . xto(B)) . C) . D)
Improved circuit
This circuit can easily be modified. What if, for example, you wanted to have an override switch (E) that allowed the lock to be opened without using the combination inputs? The function is now:
f should equal 1 if: A is 1 AND B is 0 AND C is 1 AND D is 1 OR E is 1
or
f = A . xto(B) . C . D + E
and the circuit becomes
It's a simple matter to design and build more and more complex circuits this way. As the Boolean expressions become more complex, they can be simplified using the rules of Boolean algebra or mapping techniques such as Karnaugh maps. We won't go into those here, but any introductory book on digital circuits will discuss them.
There is a more important problem that the above circuits give rise to. The diagrams show that you need to have four fingers in order to operate the switches! A more complex circuit might require you not only to have super-multi-digital hands, but also to be able to press all your finger down on the switches at exactly the same time. This would be particularly important if the circuit were designed to trigger an alarm when the wrong combination was entered. This would require nanosecond timing in order not to enter random combinations as each finger lowers onto each switch. Another problem is that the alarm would cease to ring as soon as the fingers released the switches--hardly an adequate warning device.
Time to consider sequential circuits.
B3 Sequential circuits
The output state of a sequential circuit depends, not only on the current inputs, but also on the previous inputs to the circuit (the sequence of inputs). This gives these circuits the property of memory: the output of a circuit can remain in a particular state even after the input change that put it there has long gone.
(a) Flip flops
The basic sequential circuit element is the flip-flop, often referred to as a data latch or a one-bit memory cell. You will read about various different types of flip-flops: JK flip-flop, T flip-flop, RS flip-flop, etc. We will only consider the D flip-flop here (the 'D' stands for 'data').
D-type
The D flip-flop has two inputs and two outputs. One of the inputs, D, carries the data that will end up at the output. The other input is for a clock pulse that determines when the D input state should be transferred to the output. The two outputs are compliments of each other (xto(Q) being provided for convenience).
The connections labelled S and C are also inputs of sorts. They enable the output to be 'set' (made equal to 1) and 'cleared' (made equal to 0) at any time--independent of the clock.
The clock input has a small angle bracket on it ( ) indicating that it is the edge of the clock pulse that determines when things happen. This makes for very precise timing of output changes.
Truth tables for a flip-flop must be slightly different than those for gates since we have to denote changes to inputs, not just the inputs themselves. Any changes will only happen after the arrival of a clock pulse. Hence we look at the output state (Q) of the flip-flop before the clock pulse arrives, and after the clock pulse has gone. We represent these two conditions of the output as Qt and Qt+1 respectively.
So the truth table for a D-type flip-flop is:
that is, the output takes on the value of the input after a clock pulse has occurred. This is a nice and simple truth table compared with some others. The JK flip-flop, for example, has its new output state depending on, not only the input states, but also the previous output state.
(For completion here, the JK has two inputs and its truth table and diagram are:
This is a very useful flip-flop because it provides each of the four possible results that could happen to an output:
stay the same as it was (Qt),
change to the opposite of what it was (xto(Qt))
set to 1
reset to 0
In designing a circuit you simply decide the kind of action you want and set the input values of J and K appropriately.)
One-bit memory
A D-type flip-flop is a one-bit memory cell. What ever data value (0 or 1) is applied to the input is latched at the output after the next clock pulse. And it stays there even after the input (D) changes!
(b) Register
To solve the problem of our combination lock circuit needing to hold onto its inputs, we need to string several flip-flops together. This is called a register. It lets us take our time while setting up the number we wish to try for the combination and then enter the number by clocking all the flip-flops simultaneously.
(c) Applications of a register
The register we have looked at loads all the 4 data bits in parallel. We could arrange for the data bits to be loaded into it in serial. In the circuit below they are clocked in one at a time, each one being shifted to the right as the clock pulse arrives. This circuit is referred to as a shift register.
Similarly, we could arrange for the data to be shifted out in a serial fashion. These two circuits are very common computing circuit called parallel -to-serial and serial-to-parallel converters. They are particularly useful in communication circuits where these conversions have to take place at either end of a serial line.
B4 Computing circuits
The few simple circuits we have looked at give us insight into the myriad of circuits that are used in digital computers. We have already commented on the role of shift registers in getting data into and out of computers via a serial line. They are also found in the computer chip itself. We will now briefly look at some of these circuits.
(a) Memory
Simple flip-flops are actually the basis of static RAM often used as fast RAM, or cache RAM, in a computer. It holds its data so long as the power remains on. The other (cheaper) RAM found in a computer is dynamic RAM, this is essentially an array of transistors in which charge is stored (or not stored) on their bases. Since the charge leaks off, the memory contents must be continually refreshed--hence the name dynamic.
(b) Reading and writing memory
The basic memory cell requires some simple logic to enable data to be written to it and read from it. The circuit below shows one possibility. (Actual circuits are somewhat different as they have to allow for the possibility of many memory outputs being connected together, but only one being selected at any one time. The is called 'enabling' an output.)
Data can be clocked into the flip-flop while the write switch is on 1. The output is always 0 unless the write switch is set to 0 (meaning read) and then the output reflects the value stored in the flip-flop.
In Boolean terms, this circuit can be described by:
Qt+1 = write . dataIn + xto(write) . Q
dataOut = xto(write) . Q (you can interpret xto(write) as 'read')
Check the logic for yourself.
(c) Instruction register
When the computer fetches an instruction from memory, it is stored in an instruction register. Yes, you guessed it, a simple register comprising flip-flops. This register will be 32 bits long in most desktop computers today. Once the instruction is in the register, combinational logic circuits go to work on it to decode what the instruction means.
For example, the bit pattern 1010 in a particular part of the instruction might mean 'load data from somewhere', other parts of the instruction defining where the data should be loaded from. In that case, a logic circuit would 'decode' this (ie. implement a f = A.xto(B).C.xto(D) logic function) and use the output as an input to a memory read circuit. (That's simplified somewhat, especially considering that many microprocessors have on-board 'microcode' instruction sets that do some of this work. But at the most basic level, somewhere in the chip, this sort of thing goes on.)
(d) ROMs, PROMs and PLAs
Couldn't let these notes go by without dropping a few acronyms!
A read only memory (ROM) comprises an array of memory cells containing fixed, unalterable data. Programmable read only memory (PROM) is similar but allows these data to be changed usually by applying a much higher voltage, or after exposure to ultraviolet light to erase the previous contents. These devices don't use flip-flops but either have the data 'burnt' into them in the last stage of manufacture (ROMs) or employ technology which allows a transistor to remain in a particular state for an extremely long period.
These devices have particular relevance to the digital circuits we looked at earlier. Consider the similarity between sending an address (4-bit binary word, say) to a memory device (say, a 32 word ROM) to find the contents stored at that address, and inputting values (say, the state of 4 switches) to a logic circuit to see what output it generates.
The digital circuit will output one bit in response to the 4-bit input. The ROM will output 5 bits in response to the 4-bit input. These 5 bits could be the outputs of 5 related or independent logic functions:
 In other words, a memory device can be used as a way of implementing some pretty complex logic functions--and it can be re programmable to!
In other words, a memory device can be used as a way of implementing some pretty complex logic functions--and it can be re programmable to! This is commonly done these days. Such devices are called programmable logic arrays are a nothing more than ROMs or PROMs programmed to emulate specific logic functions. They are often used to implement to numerous 'glue' logic circuits which tie together various logic chips in a computer.
Part C. Resources
A few resources for you to follow up on some of this work.
C1 Analogue & Digital Electronics
A few generally helpful books:
W L Faissler, An Introduction to Modern Electronics, Wiley, 1991.
W F Stubbins, Essential Electronics, Wiley, 1986.
M H Jones, A Practical Introduction to Electronic Circuits, CUP 1985
P Horowitz & W Hill, The Art of Electronics, CUP, 1990
Wave Window Au
C2 Digital Electronics
A really practical book is:
D Lancaster, TTLCookbook , Howard Sams & Co, 1980 (there is probably a more recent edition by now!).
C3 Computer software
The following software is mainly for the Macintosh computer. I couldn't find any really useful shareware programs for the PC. Please let me know if you know of any.
The diagrams in these notes were made using SimLog. This digital circuit simulator is available from Oxford United Press (253 Normanby Rd, South Melbourne, 3205, tel. 646 4200. $240). A demonstration copy of this software is included of the accompanying Macintosh disc. It has some features disabled.
Lecture demonstrations also made use of DigSim, a shareware simulator (included on the accompanying Macintosh disc).
A commercial program Electronic Workbench (for both PC and Mac) offers both digital and analogue simulations. Available from Emona Instruments, PO Box 15, Camperdown, NSW 2050, (02) 519 3933.
MicroCap IV for the PC offers anlaogue simulation. A student version is avaliable for about $65 (limited number of connections). Distributed by Addison-Wesley.
C4 Lecture presentation software.
The lecture was presented using PowerPoint and HyperCard. The simulations in the Hypercard stack are available on the accompanying disc. They are intended for lecture presentation, not student use. This means they should not be treated as accurate, user-friendly simulations, but rather, as a way of presenting some ideas visually.
C5 Amplifier board
For those interested, we can supply a printed circuit board on which you can construct the three op amp circuits. The circuits are a unity gain buffer, a differential amp (with provision for a pot to set a DC offset to one input) and a variable gain amp (from 1 to 1000 gain).
(a) Description of the board
The board has been designed to run from single supply (5 to 16 volt) or dual supply (+/-8.5 volt). There is provision for a voltage divider near the input to the first amp (for a transducer to be attached) and trim pots on each amp to adjust input voltage offsets. Sockets to accept wire links (telecom wire) allow you to connect the amps together in various ways.
The cost of the board is about $7 and the components (which you must purchase for yourself) will cost about $30.
(b) Constructing the board
It's straightforward. Drill holes for the components, solder in the IC sockets, fixed resistors, multiturn pots, capacitors, sockets and the one wire link.
If you wish to run from a single supply (say, a 9 volt battery) then link the earth and negative rails together with a wire link (bottom two rails of the board).
If running from a dual supply using two 9 volts batteries, then you should put a diode in series with each power rail to drop the voltage by about 0.6 volts (the maximum supple voltage for dual supply is 8.5 volts).
Insert the op amp ICs. Handle them with care as they are liable to damage from static electricity.
(c) Setting it up
Adjusting voltage offset
For each amplifier in turn, connect its input(s) to earth, and adjust each offset trim pot to give you as close to 0 volts at the output as possible (should be able to get under 1 millivolt).
Setting amplifier gain
The final amp has a multiturn trim pot (RV4) with which you can adjust its gain. The maximum gain will be (1 + value of RV4 in k[[Omega]]); ie. a 500 k[[Omega]] put will give a maximum gain of 501.
To set the gain to a particular value (say, 100), set the output of pot RV5 to a convenient value (say, 20 millivolts) and adjust the gain pot (RV4) until the output is correct (2.00 volts, in this case).
(d) Component list
Resistors
7 at 100 k[[Omega]]
Multiturn trim pots (top adjust)
1 at 10 k[[Omega]]
3 at 100 k[[Omega]]
1 at 500 k[[Omega]] or 1 M[[Omega]]
Capacitors
2 at 10 uF (tantalum)
ICs
3 at CA3160E
Wave Window Washing
Other
3 IC sockets (8 pin)
about 23 single pin sockets
2 diodes
| [Back to J Pearce Home Page] |
These pages are maintained by Jon Pearce ( jonmp@unimelb.edu.au), Department of Information Systems. The opinoins on them do not necessarily reflect those of the University of Melbourne. Tel: (613) 8344 1495 Fax: (613) 9349 4596. Last update: September 16, 2003 .
